In my CSI 2050 class at MSCD, my professor Judith Gurka showed me the cover of the book Algorithms by Robert Sedgewick. The cover shows a picture of insertion sort in action—sort of a rising staircase of sorted values pushing its way through unsorted confusion. I decided to make similar pictures of other sorting algorithms. (I couldn't find a picture of the cover online, but it looks a lot like my insertion sort picture below, only it goes from right to left.)
I wrote a Python program that emits PostScript. The pictures below were rasterized with Ghostscript. Wikipedia's sorting algorithm article gave me ideas for which sorts to do.
Interestingly, it appears Sedgewick has given a talk on Visualizing the Analysis of Algorithms; he suggests using PostScript for this kind of thing.
It's tempting to compare the performance of these algorithms just by comparing the widths of their respective diagrams, but don't do that. Doing this would make bubble sort look faster that heapsort, which it is not. The reason is that while the columns in the diagrams each represent one "pass" of the algorithm, not all passes represent the same amount of work.
You can click on the diagrams to download them in EPS format.
Here are all the diagrams with labels for letter-sized paper.
See also: Visualizing Sorting Algorithms by Also Cortesi. It is a similar idea, however individual elements are connected from one step to the next, so you can trace them throughout the whole execution.
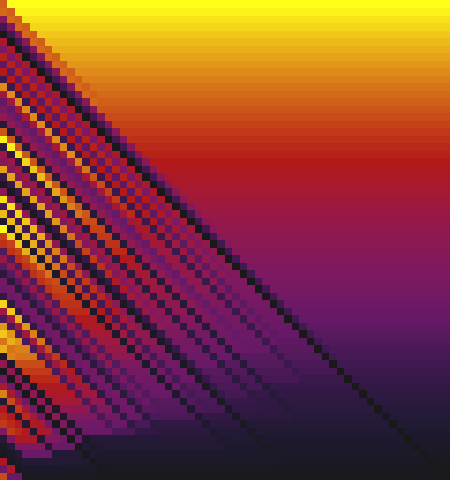
Bubble sort. Here you can see how bubble sort is limited by the element that is farthest above its proper place.

Bidirectional bubble sort. This picture was the most surprising to me. I hadn't previously considered that elements that aren't the smallest or largest in each pass just wobble back and forth until they are picked. It's also interesting to see graphically how much more quickly it terminates than plain bubble sort.

Insertion sort. This is just like the cover of Sedgewick's book.

Shell sort. You can see the step sizes shrinking until insertion sort is performed on an almost-sorted list.
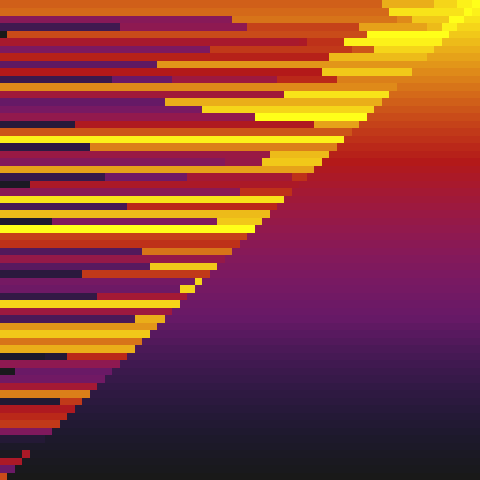
Selection sort. This one is pretty boring.
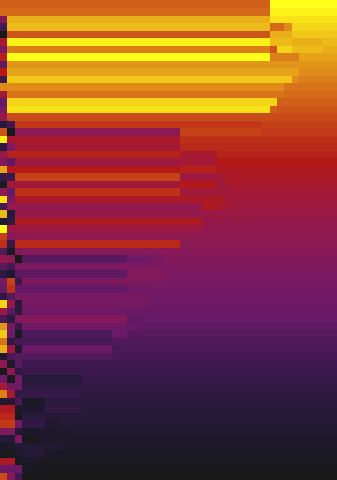
Quicksort. You can see that after partitioning, the pivot element is in its proper place and stays there until the end.

Merge sort. This one makes a nice picture. The only real work is done during the merge step. Notice that the list is totally wrong all the way up to the final merge.

Heapsort. The first third of the diagram is the creation of the heap.